PMN and PQR are two secants of the circle MQTRN... - JAMB Mathematics 1991 Question
A
7.3, 5.9
B
7.7, 12.5
C
12.5, 7.7
D
5.9, 7.3
correct option: c
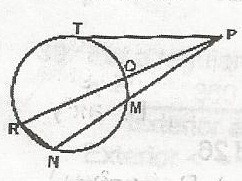
\(\frac{PQ}{PN} = \frac{PM}{PR} = \frac{QM}{NR}\)
\(\frac{4.8}{12} = \frac{5}{PR}\)
PR = \(\frac{5 \times 12}{4.8} = \frac{50}{4}\)
= 12.5
\(\frac{PQ}{PN} = \frac{PM}{PT} = \frac{TM}{NT}\)
\(\frac{PT}{12} = \frac{5}{PR}\)
PT2 = 60
PT = \(\sqrt{60}\)
= 7.746
= 7.7
\(\frac{4.8}{12} = \frac{5}{PR}\)
PR = \(\frac{5 \times 12}{4.8} = \frac{50}{4}\)
= 12.5
\(\frac{PQ}{PN} = \frac{PM}{PT} = \frac{TM}{NT}\)
\(\frac{PT}{12} = \frac{5}{PR}\)
PT2 = 60
PT = \(\sqrt{60}\)
= 7.746
= 7.7
Please share this, thanks:
Add your answer
No responses